¿Cómo se resuelve los números consecutivos. Novedad aquí - ¿Cuál es la fórmula para sumar números consecutivos

Veamos un ejemplo: Si queremos sumar los 100 primeros números: n = 100, luego: Suma = (100·(101))/2 = 10100/2 = 5050.

Tres números consecutivos son aquellos que siguen el uno al otro en orden, sin saltos. Por tanto, podemos denominar tres números consecutivos como , y . Nos dicen que la suma de dichos números es 219, por tanto: Los número buscados serán 72, 73 y 74.

12, 13, 14 y 15 son números consecutivos.

ÍNDICE DE INICIACIÓN AL ÁLGEBRA. ... 1. Sea x un número cualquiera. Escribir las siguientes expresiones mediante lenguaje algebraico.

Expresión escrita	Expresión algebraica
El anterior o antecesor de x (x∈Ζ)	x - 1
Tres números consecutivos cualesquiera	x , (x + 1) , (x + 2) , o bien, (x - 1) , x , ( x + 1)

¿Cuánto suma los números consecutivos del 1 al 100

Carl Friedrich Gauss obtuvo la respuesta casi de inmediato: 1 + 2 + 3 + … + 99 + 100 = 5050.» Una historia mil veces contada. Todos los profesores de primaria y secundaria se la cuentan a sus alumnos.

¿Cómo sumar 365 números consecutivos

1:48Sugerencia de vídeo · 51 segundos¿CUÁNTO ES 1+2+3+... HASTA 365 ¿Cómo sumarlo todo de ... - YouTube

Por tanto, los tres números consecutivos que suman 219 son 72, 73 y 74.

Respuesta: -4, -3, -2, -1, 0, 1 , 2, 3...

¿Cuánto es 1 2 3 4 hasta el 100

1:48Sugerencia de vídeo · 51 segundos¿CUÁNTO ES 1+2+3+... HASTA 365 ¿Cómo sumarlo todo de ... - YouTube

17. Calcula el número natural que sumado a su siguiente da 157. x + (x + 1) = 157 → x = 78. El número es 78.

La respuesta que Gauss dio fue: 5050.

Los números consecutivos son números que, al contar, se suceden uno al otro y están en orden. Por ejemplo: 1, 2, 3, 4…, o 59, 58, 57, 56… También podemos dividirlos entre números pares consecutivos y números impares consecutivos.Según la Real Academia Española, consecutivo significa que sigue inmediatamente a otra cosa o es consecuencia de ella.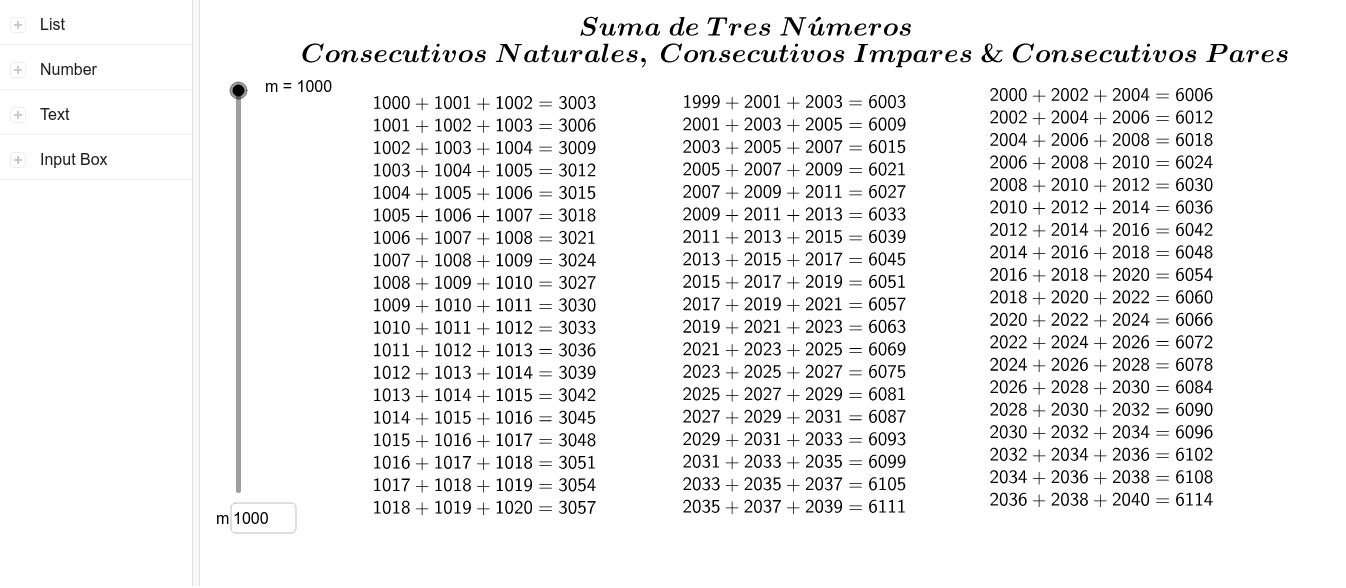

¿Cuál es la suma de tres números consecutivos

0:19Sugerencia de vídeo · 54 segundos(3) Suma de 3 NÚMEROS CONSECUTIVOS. Problemas con ...Carl Friedrich Gauss obtuvo la respuesta casi de inmediato: 1 + 2 + 3 + … + 99 + 100 = 5050.» Una historia mil veces contada. Todos los profesores de primaria y secundaria se la cuentan a sus alumnos.La respuesta que Gauss dio fue: 5050. Si hacéis esas 99 sumas de las que habíamos hablado llegareis a esa solución, aunque tardando bastante más de lo que tardó aquel joven muchacho. Sin duda es sorprendente la rapidez con la que Gauss dio la respuesta correcta, y más aún teniendo en cuenta que tan solo tenía 9 años.Carl Friedrich Gauss obtuvo la respuesta casi de inmediato: 1 + 2 + 3 + … + 99 + 100 = 5050.» Una historia mil veces contada.Para hallar la suma de los números consecutivos del 1 al 100, tendrás que multiplicar la cantidad de pares (50) por la suma de cada par (101): {\displaystyle 101(50)=5050.} Por lo tanto, la suma de los números consecutivos del 1 al 100 es 5050.

¿Cómo son los consecutivos

¿Cuándo dos ángulos son consecutivos Dos ángulos son consecutivos cuando tienen en común el vértice y uno de sus lados.

El concepto se emplea para nombrar a aquello que sucede o aparece a continuación de otra cosa de forma inmediata o sin interrupciones.

consecutivo, -va Que sigue a otra cosa inmediatamente.

La respuesta que Gauss dio fue: 5050.1 one, 2 two, 3 three, 4 four, 5 five, 6 six, 7 seven, 8 eight, 9 nine, 10 ten, 11 eleven, 12 twelve, 13 thriteen, 14 fourteen, 15 fifteen, 16 sixteen, 17 seventeen, 18 eighteen, 19 nineteen, 20 twenty. Como pudiste notar son números bastante sencillos, los cuales puedes memorizar con facilidad.